Earlier today, the Earth was at the point in its elliptical orbit closest to the Sun – the perihelion.
The featured image is the Sun at around the time of today’s perihelion as viewed by NASA’s Solar Dynamics Observatory.
The Earth’s orbit is only very slightly elliptical. Its semi-major axis (half the long axis of the ellipse) is 149.6 million kilometres, but as its eccentricity is only 0.01671123, the semi-minor axis is only about 21,000 km smaller. It’s very hard to spot that this is an ellipse rather than a perfect circle.
The Sun lies at one focus of this elliptical orbit, offset 2.5 million kilometres from the centre*. So, on one side of its orbit (at perihelion), the Earth is 5 million kilometres closer to the Sun than on the opposite side (aphelion).
I thought I’d try illustrating this with a properly scaled drawing.
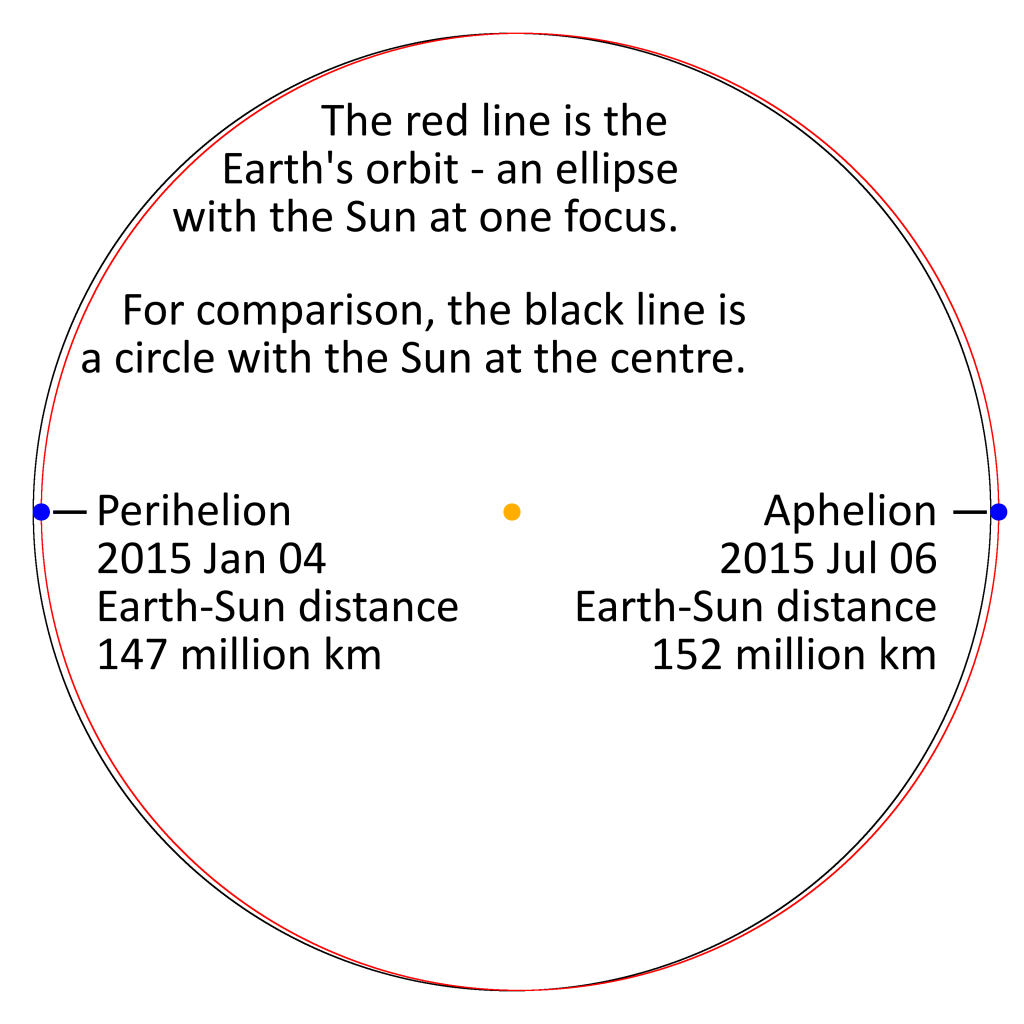 You can find perihelion and aphelion dates and details on the USNO website.
You can find perihelion and aphelion dates and details on the USNO website.
* The separation of focus and centre is given by the product of the eccentricity and the semi-major axis.


4 responses to “Perihelion”
Great to know it ! what about the effect of this perihilion on out planet ?!
The effect is fairly small, albeit not negligible. The amount of energy reaching the Earth from the Sun goes as the inverse square of distance. So there is (1/147)^2 / (1/152)^2 = (152/147)^2 = 1.069 more energy intercepted by the Earth at perihelion than at aphelion i.e. about 7% more.
why are planetary orbits elliptical, and are all orbiting bodies orbits elliptic; i.e. stars around black holes, moons around planets?
Hi, the central 1/r^2 nature of gravitational force leads to an orbit which is a conic section (circle, ellipse, parabola, hyperbola)